Axioms, Properties and Definitions of Real Numbers

Axioms, Properties and Definitions of Real Numbers

 

 

Definitions

 

1.Property of a number system–a fact that is true regarding that system

 

2.Axiom–a property that forms the framework for the system. It does not require any proof. We assume that it is true.

 

   3.Term–a combination of numbers and variables that are multiplied together.

 

4.Like terms–two or more terms that have the identical variables raised to the same power(s).

 

 5.Coefficient–the number multiplying a variable in a term.If there is no written number, it is assumed to be 1.

 

  6.Expression–a combination of terms added together

 

7.Equation–A combination of terms added together that contains an equal sign

 

  8.Inequality–A combination of terms added together that contains an greater than, less than, greater than or equal to, less than or equal  to.

 

9.Factor–a combination of numbers and variables that divides into a term evenly.

 

10.Common Factor–a combination of numbers and variables that is a factor of each in an expression

Field Axioms/Properties (1)

Properties of Real Numbers

The following table lists the defining properties of the real numbers (technically called the field axioms). These laws define how the things we call numbers should behave.

Addition	Multiplication
Commutative For all real a, b a + b = b + a	Commutative For all real a, b ab = ba
Associative For all real a, b, c a + (b + c) = (a + b) + c	Associative For all real a, b, c (ab)c = a(bc)
Identity There exists a real number 0 such that for every real a a + 0 = a	Identity There exists a real number 1 such that for every real a a × 1 = a
Additive Inverse (Opposite) For every real number a there exist a real number, denoted (-a), such that a + (–a) = 0	Multiplicative Inverse (Reciprocal) For every real number a except 0 there exist a real number, denoted , such that a ×  = 1
Distributive Law For all real a, b, c a(b + c) = ab + ac, and (a + b)c = ac + bc

The commutative and associative laws do not hold for subtraction or division:

a – b is not equal to b – a

a ÷ b is not equal to b ÷ a

a – (b – c) is not equal to (a – b) – c

a ÷ (b ÷ c) is not equal to (a ÷ b) ÷ c

Try some examples with numbers and you will see that they do not work.

What these laws mean is that order and grouping don't matter for addition and multiplication, but they certainly do matter for subtraction and division. In this way, addition and multiplication are “cleaner” than subtraction and division. This will become important when we start talking about algebraic expressions. Often what we will want to do with an algebraic expression will involve rearranging it somehow. If the operations are all addition and multiplication, we don't have to worry so much that we might be changing the value of an expression by rearranging its terms or factors. Fortunately, we can always think of subtraction as an addition problem (adding the opposite), and we can always think of division as a multiplication (multiplying by the reciprocal).
You may have noticed that the commutative and associative laws read exactly the same way for addition and multiplication, as if there was no difference between them other than notation. The law that makes them behave differently is the distributive law, because multiplication distributes over addition, not vice-versa.. The distributive law is extremely important, and it is impossible to understand algebra without being thoroughly familiar with this law.
Example:  2(3 + 4)
According to the order of operations rules, we should evaluate this expression by first doing the addition inside the parentheses, giving us

2(3 + 4) = 2(7) = 14

But we can also look at this problem with the distributive law, and of course still get the same answer. The distributive law says that

Mindanao: The Catacomb Of Peace - Poem by Antonio Liao

 take me where the ingredients of lewd peace
live, fun me to the shore of sweet embrace
for nothing left with me, but pain and
aspiration to remember the past of excitement

the abundance of milk and honey, capture the
challenge of culture imprison each desire
to the quest of destiny, haul only with faded
hope emptied by sporadic clashes of fear and
discouragement to settle in the light of
discontentment and failure

oh! wealth of many faces, gain and live by
leaches of the politician, help me find my
feet, while the tongue wait to find the
little hand that the brain focus, has install
the courage to wake the deep close eyes that
seldom glimpse of hunger

alas! the dawn finds and settles down each dye
of darkness to glow of blooming daylight zone
to live ...

Literature

Submitted by: Rea Ylanan

 Submitted to: Romeo Fabales

Mathematics (Part 2:All About Algebraic Expression)

 Topic in Mathematics Search by: Rea Ylanan

Instructor: Ar-jay Ylalim

Product Rule

The product rule is one of several rules used to find the derivative of a function. Specifically, it is used to find the derivative of the product of two functions. It is also called Leibnitz's Law, and it states that for two functions f and g their derivative (in Leibnitz notation, ). The derivative of f times g is not equal to the derivative of f times the derivative of g: . The product rule can be used with multiple functions and is used to derive the power rule. The product rule can also be applied to dot products and cross products of vector functions. The Leibnitz Identity, a generalization of the product rule, can be applied to find higher-order derivatives.

Quotient rule

 In calculus, the quotient rule is a method of finding the derivative of a function that is the quotient of two other functions for which derivatives exist

If the function one wishes to differentiate, ${\displaystyle f(x)}$, can be written as

${\displaystyle f(x)={\frac {g(x)}{h(x)}}}$

and ${\displaystyle h(x)\not =0}$, then the rule states that the derivative of ${\displaystyle g(x)/h(x)}$ is

${\displaystyle f'(x)={\frac {g'(x)h(x)-h'(x)g(x)}{[h(x)]^{2}}}.}$

Many people remember the Quotient Rule by the rhyme "Low D-high, High D-low, cross the line and square the low." It is important to remember the 'D' describe the succeeding portion of the original fraction.

 

 Synthetic Division: The Process

 Synthetic division is a shorthand, or shortcut, method of polynomial division in the special case of dividing by a linear factor -- and it only works in this case. Synthetic division is generally used, however, not for dividing out factors but for finding zeroes (or roots) of polynomials. More about this later.
If you are given, say, the polynomial equation y = x² + 5x + 6, you can factor the polynomial as y = (x + 3)(x + 2). Then you can find the zeroes of y by setting each factor equal to zero and solving. You will find that x = –2 and x = –3 are the two zeroes of y.

You can, however, also work backwards from the zeroes to find the originating polynomial. For instance, if you are given that x = –2 and x = –3 are the zeroes of a quadratic, then you know that x + 2 = 0, so x + 2 is a factor, and x + 3 = 0, so x + 3 is a factor. Therefore, you know that the quadratic must be of the form y = a(x + 3)(x + 2).

	ADVERTISEMENT

(The extra number "a" in that last sentence is in there because, when you are working backwards from the zeroes, you don't know toward which quadratic you're working. For any non-zero value of "a", your quadratic will still have the same zeroes. But the issue of the value of "a" is just a technical consideration; as long as you see the relationship between the zeroes and the factors, that's all you really need to know for this lesson.)
Anyway, the above is a long-winded way of saying that, if x – n is a factor, then x = n is a zero, and if x = n is a zero, then x – n is a factor. And this is the fact you use when you do synthetic division.

Let's look again at the quadratic from above: y = x² + 5x + 6. From the Rational Roots Test, you know that ± 1, 2, 3, and 6 are possible zeroes of the quadratic. (And, from the factoring above, you know that the zeroes are, in fact, –3 and –2.) How would you use synthetic division to check the potential zeroes? Well, think about how long polynomial divison works. If we guess that x = 1 is a zero, then this means that x – 1 is a factor of the quadratic. And if it's a factor, then it will divide out evenly; that is, if we divide x² + 5x + 6 by x – 1, we would get a zero remainder. Let's check:
As expected (since we know that x – 1 is not a factor), we got a non-zero remainder. What does this look like in synthetic division? Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

First, write the coefficients ONLY inside an upside-down division symbol:
Make sure you leave room inside, underneath the row of coefficients, to write another row of numbers later.
Put the test zero, x = 1, at the left:
Take the first number inside, representing the leading coefficient, and carry it down, unchanged, to below the division symbol:
Multiply this carry-down value by the test zero, and carry the result up into the next column:
Add down the column:
Multiply the previous carry-down value by the test zero, and carry the new result up into the last column:
Add down the column: This last carry-down value is the remainder.

Comparing, you can see that we got the same result from the synthetic division, the same quotient (namely, 1x + 6) and the same remainder at the end (namely, 12), as when we did the long division:
The results are formatted differently, but you should recognize that each format provided us with the result, being a quotient of x + 6, and a remainder of 12.

You already know (from the factoring above) that x + 3 is a factor of the polynomial, and therefore that x = –3 is a zero. Now compare the results of long division and synthetic division when we use the factor x + 3 (for the long division) and the zero x = –3 (for the synthetic division):

As you can see above, while the results are formatted differently, the results are otherwise the same:
In the long division, I divided by the factor x + 3, and arrived at the result of x + 2 with a remainder of zero. This means that x + 3 is a factor, and that x + 2 is left after factoring out the x + 3. Setting the factors equal to zero, I get that x = –3 and x = –2 are the zeroes of the quadratic.
In the synthetic division, I divided by x = –3, and arrived at the same result of x + 2 with a remainder of zero. Because the remainder is zero, this means that x + 3 is a factor and x = –3 is a zero. Also, because of the zero remainder, x + 2 is the remaining factor after division. Setting this equal to zero, I get that x = –2 is the other zero of the quadratic.
I will return to this relationship between factors and zeroes throughout what follows; the two topics are inextricably intertwined.

Mathematics (Part 1:All About Algebraic Expression)

Algebraic expression

"Rational expression" redirects here. For the notion in formal languages, see regular expression.

In mathematics, an algebraic expression is an expression built up from integer constants, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number).^[1] For example, ${\displaystyle 3x^{2}-2xy+c}$ is an algebraic expression. Since taking the square root is the same as raising to the power ${\displaystyle {\tfrac {1}{2}}}$,

${\displaystyle {\sqrt {\frac {1-x^{2}}{1+x^{2}}}}}$

is also an algebraic expression. By contrast, transcendental numbers like π and e are not algebraic.
A rational expression is an expression that may be rewritten to a rational fraction by using the properties of the arithmetic operations (commutative properties and associative properties of addition and multiplication, distributive property and rules for the operations on the fractions). In other words, a rational expression is an expression which may be constructed from the variables and the constants by using only the four operations of arithmetic. Thus, ${\displaystyle {\frac {3x^{2}-2xy+c}{y^{3}-1}}}$ is a rational expression, whereas ${\displaystyle {\sqrt {\frac {1-x^{2}}{1+x^{2}}}}}$ is not.
A rational equation is an equation in which two rational fractions (or rational expressions) of the form ${\displaystyle {\frac {P(x)}{Q(x)}}}$ are set equal to each other. These expressions obey the same rules as fractions. The equations can be solved by cross-multiplying. Division by zero is undefined, so that a solution causing formal division by zero is rejected.

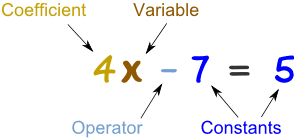
1. Addition and Subtraction of Algebraic Expressions

Before we see how to add and subtract integers, we define terms and factors.

Terms and Factors

A term in an algebraic expression is an expression involving letters and/or numbers (called factors), multiplied together.

Example 1

The algebraic expression

5x

is an example of one single term. It has factors 5 and x.
The 5 is called the coefficient of the term and the x is a variable.

Example 2

5x + 3y has two terms.

First term: 5x, has factors $\displaystyle{5}$5 and x
Second term: 3y, has factors $\displaystyle{3}$3 and y

The $\displaystyle{5}$5 and $\displaystyle{3}$3 are called the coefficients of the terms.

Example 3

The expression

$\displaystyle{3}{x}^{2}-{7}{a}{b}+{2}{e}\sqrt{{\pi}}$3x​2​​−7ab+2e√​π​​​

has three terms.

First term: $\displaystyle{3}{x}^{2}$3x​2​​ has factors $\displaystyle{3}$3 and x²
Second term: $\displaystyle-{7}{a}{b}$−7ab has factors $\displaystyle-{7}$−7, a and b
Third Term: $\displaystyle{2}{e}\sqrt{{\pi}}$2e√​π​​​; has factors $\displaystyle{2}$2, $\displaystyle{e}$e, and $\displaystyle\sqrt{{\pi}}$√​π​​​.

The $\displaystyle{3}$3, $\displaystyle-{7}$−7 and $\displaystyle{2}$2 are called coefficients of the terms.

Like Terms

"Like terms" are terms that contain the same variables raised to the same power.

Example 4

3x² and 7x² are like terms.

Example 5

-8x² and 5y² are not like terms, because the variable is not the same.

Adding and Subtracting Terms

Important: We can only add or subtract like terms.
Why? Think of it like this. On a table we have 4 pencils and 2 books. We cannot add the 4 pencils to the 2 books - they are not the same kind of object.
We go get another 3 pencils and 6 books. Altogether we now have 7 pencils and 8 books. We can't combine these quantities, since they are different types of objects.
Next, our sister comes in and grabs 5 pencils. We are left with 2 pencils and we still have the 8 books.
Similarly with algebra, we can only add (or subtract) similar "objects", or those with the same letter raised to the same power.

Example 6

Simplify 13x + 7y − 2x + 6a 
~answer:
13x + 7y − 2x + 6a
The only like terms in this expression are $\displaystyle{13}{x}$13x and $\displaystyle-{2}{x}$−2x. We cannot do anything with the $\displaystyle{7}{y}$7y or $\displaystyle{6}{a}$6a.
So we group together the terms we can subtract, and just leave the rest:

(13x − 2x) + 6a + 7y
= 6a + 11x + 7y

Types of Algebraic Expressions

Types of algebraic expressions may further be distinguished in the following five categories.

They are: monomial, polynomial, binomial, trinomial, multinomial.

1. Monomial: An algebraic expression which consists of one non-zero term only is called a monomial.
Examples of monomials:
a is a monomial in one variable a.
10ab² is a monomial in two variables a and b.

5m²n is a monomial in two variables m and n.

-7pq is a monomial in two variables p and q.

5b³c is a monomial in two variables b and c.

2b is a monomial in one variable b.

2ax/3y is a monomial in three variables a, x and y.

k² is a monomial in one variable k.
2. Polynomial: An algebraic expression which consists of one, two or more terms is called a polynomial.
Examples of polynomials:
2a + 5b is a polynomial of two terms in two variables a and b.
3xy + 5x + 1 is a polynomial of three terms in two variables x and y.
3y⁴ + 2y³ + 7y² - 9y + 3/5 is a polynomial of five terms in two variables x and y.

m + 5mn – 7m²n + nm² + 9 is a polynomial of four terms in two variables m and n.

3 + 7x⁵ + 4x² is a polynomial of three terms in one variable x.

3 + 5x² - 4x²y + 5xy² is a polynomial of three terms in two variables x and y.

x + 5yz – 7z + 11 is a polynomial of four terms in three variables x, y and z.

1 + 2p + 3p² + 4p³ + 5p⁴ + 6p⁵ + 7p⁶ is a polynomial of seven terms in one variable p.
3. Binomial: An algebraic expression which consists of two non-zero terms is called a binomial.
Examples of binomials:
m + n is a binomial in two variables m and n.
a² + 2b is a binomial in two variables a and b.

5x³ – 9y² is a binomial in two variables x and y.

-11p – q² is a binomial in two variables p and q.

b³/2 + c/3 is a binomial in two variables b and c.

5m²n² + 1/7 is a binomial in two variables m and n.
4. Trinomial: An algebraic expression of three non-zero terms only is called a trinomial.
Examples of trinomial:
x + y + z is a trinomial in three variables x, y and z.
2a² + 5a + 7 is a trinomial in one variables a.

xy + x + 2y² is a trinomial in two variables x and y.

-7m⁵ + n³ – 3m²n² is a trinomial in two variables m and n.

5abc – 7ab + 9ac is a trinomial in three variables a, b and c.

x²/3 + ay – 6bz is a trinomial in five variables a, b, x, y and z.
5. Multinomial: An algebraic expression of two terms or more than three terms is called a multinomial.
Note: binomial and trinomial are the trinomials.

Examples of multinomial:
p + q is a multinomial of two terms in two variables p and q.
a + b + c is a multinomial of three terms in three variables a, b and c.
a + b + c + d is a multinomial of four terms in four variables a, b, c and d.
x⁴ + 2x³ + 1/x + 1 is a multinomial of four terms in one variable x

a + ab + b² + bc + cd is a multinomial of five terms in four variables a, b, c and d.

5x⁸ + 3x⁷ + 2x⁶ + 5x⁵ - 2x⁴ - x³ + 7x² - x is a multinomial of eight terms in one variable x.

Like and Unlike Terms

In this section we will discuss about like and unlike terms in solving algebraic expressions.

Like terms : The terms having the same literal (variable) with same exponents are called Like terms.

Example: 1) 12x and -5x 2) 4x ² and ½ x ²

Unlike terms : The terms having the same variable with different exponents or different variable with same exponents are called Unlike terms .

Example : 1) 5x and 5y 2) 2x ² and 3y ²

Some more examples :

1)In the algebraic expression 5x ² y + 7xy ² -3xy – 4yx ²

Like terms	5x2y and – 4yx2
Unlike terms	7xy2 and -3xy

2)In the algebraic expression a ² - 3b ² + 7b ² - 9a ² + 6ab + 5

Like terms	Unlike terms
a2 and - 9a2	a2and 6ab
- 3b2 and 7b2	7b2

3)

Like terms	Unlike terms	Reason
	16x; 16y	Variables are not same
x2y ; -7x2y	-	Variables as well as exponents are same
-	9ab ; - 6b	1st term contains ab and 2nd term contains 'b' only

Variable

A symbol for a number we don't know yet. It is usually a letter like x or y.

Example: in x + 2 = 6, x is the variable.

 

Numerical Coefficient

Definition of Numerical Coefficient

The constant multiplicative factors attached to the variables in an expression are known as Numerical Coefficient.

More About Numerical Coefficient

The Numerical Coefficient is always written in front of the variable as shown in the expression given below:
a₁x₁ + a₂x₂ + ................a_nx_n where a₁,a₂...................,a_n are numerical coefficients.
Numerical Coefficient is more frequently referred as Coefficient.

Example of Numerical Coefficient

The numerical coefficient for the term 10x⁴ is 10.
The numerical coefficients for the expression 3x² + x + 1 are 3, 1, and 1.